Triangulation activity and tutorial

The resource provides a tool to play with triangulation and a tutorial on how to perform triangulation mathematically.

Some possible learning outcomes objectives that could use this tool:

• What are map grid coordinates and how do they function?
• What is the purpose of triangulation?
• How is triangulation performed?
• How does error or uncertainty accumulate in spatial measurements?
• How can points be converted to a polygon (The convex hull Quickhull algorithm)?

The tool should be optimally completed in conjunction with a grid map containing row-column identifiers, and a compass to triangulate locations with the assistance of a partner (or two observations from different locations). Aside from strengthening understanding of how triangulation works, the tool also helps to communicate how various angles of observation can impact the shape and size of uncertainty.

Additionally, the resource provides a detailed explanation of the mathematics of triangulation. The explanation provides many of the fundamentals supported with diagrams.

Grid maps

This activity can serve as a follow up resource to introducing map grids. Have students see that grid maps use incremented rows and columns of letters and/or numbers to identify grid cells. Using these it is possible to identify locations in space using codes. This of course is similar to students learning about Cartesian coordinates.

Outdoor activity

Used in conjunction with grid maps and compasses, pairs can locate themselves at a distance from one another and identify landmarks. By both students providing their position the bearing of particular landmarks, students can either calculate the triangulation manually or use Rusttrian to locate landmarks on their map.

This could be quite effectively done with a campus map with a grid overlay.

Virtual environment activity

If your lab contains virtual environments (i.e. games) that contain outdoor terrain, maps, and compasses (which is common) you can also operate the tool indoors as part of a larger lesson.

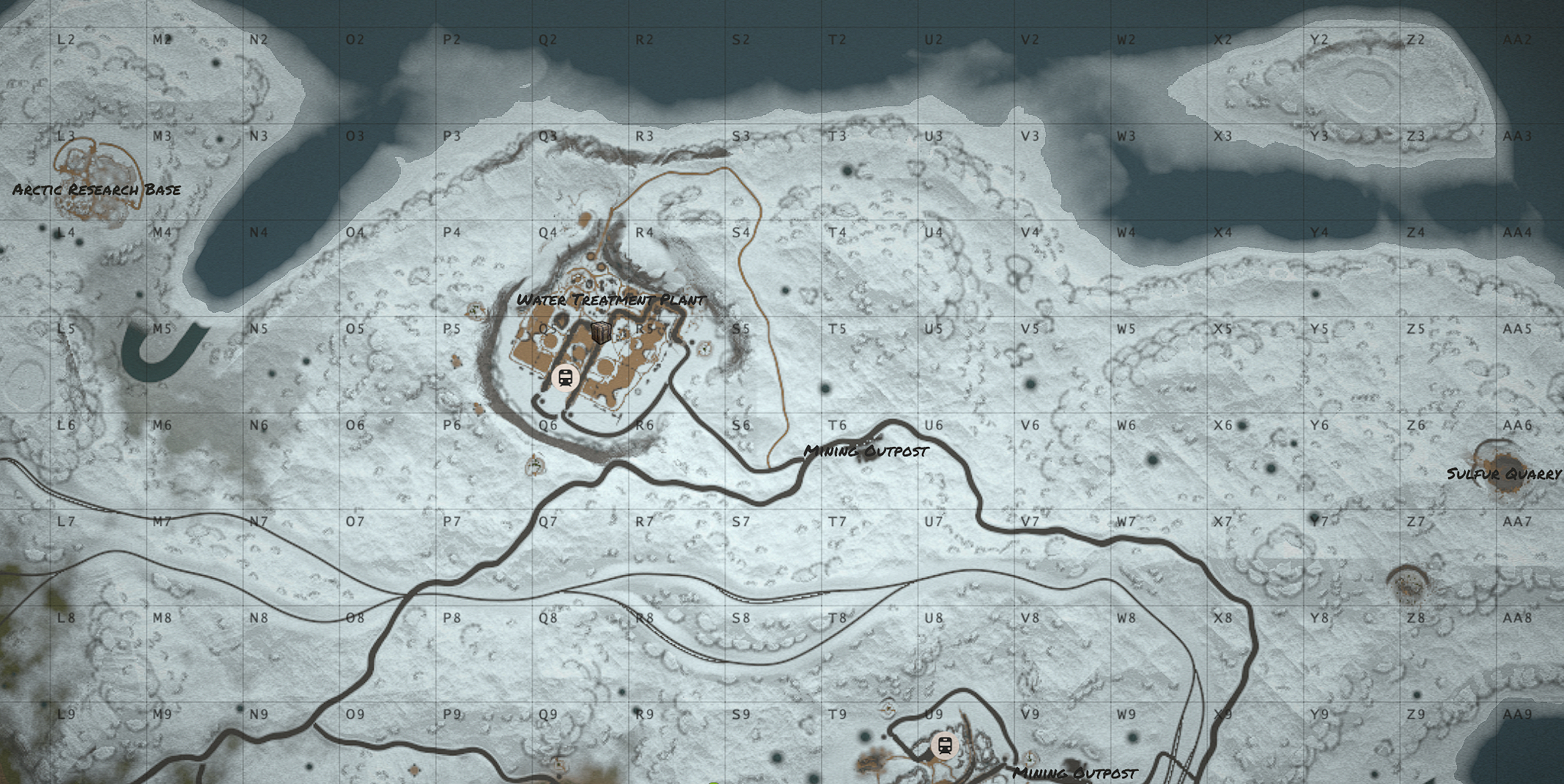
Either in a virtual environment (in games such as Rust, Minecraft, etc...) or using the map below, students could be asked to locate features given two located observations.

Desk exercise with paper maps, protractor

So for the map below, given two observers seeing supplies being parachuted down from the following locations and bearings:

• Observer 1: At the center of grid P3 and at bearing 110°
• Observer 2: At in the southwest corner of grid S8 and at bearing 35°

Given this information, within what grid is the supply drop landing?

Using the tool it should be clear that the supply drop should land near the centre of grid U5.

Present students with a series of such questions, providing location and bearing pairs, asking the students where the feature in question falls.

• Have them first use a protractor, drawing the lines on the map and seeing where they instersect.
• Then have students use Rusttrian to see how areas, rather than just points can well represent the uncertainty of locating features.